利率模拟- MATLAB & Simulink - 卡塔尔世界杯8强比赛直播

模拟利率

用插值法模拟利率

所有模拟方法都要求您通过指定周期数(NPeriods)．还可以指定严格为正的时间增量的标量或向量(DeltaTime)和中间时间步长(NSteps)．这些参数，以及与对象相关的初始采样时间(开始时间)，唯一地确定状态向量采样的时间序列。因此，模拟方法允许您从头到尾遍历时间网格(也就是说，从左到右)。

相比之下，插值方法允许您以任何顺序遍历时间网格，允许时间向前和向后移动。它们允许你指定插值次数的向量，其元素不必是唯一的。

许多参考文献将布朗桥定义为一个条件模拟结合了穿越时间网格的方案，有效地合并了两种不同的算法。相比之下，这里提供的插值方法通过有意分离算法提供了额外的灵活性。在这种沿时间网格移动的方法中，首先进行初始蒙特卡罗模拟，对终端时间的状态进行采样，然后通过随机插值对中间状态进行连续采样。最初的几个样本决定路径的整体行为，而后面的样本逐步细化结构。这种算法经常被称为方差减少技术．当插值次数为2的幂时，该算法很简单。在这种情况下，每个插值都位于两个已知状态之间，使用类似于平分的方法来改进插值。这个例子通过实现这种2的幂算法，突出了精细插值的灵活性。

加载数据。加载三个月Euribor利率历史数据集，每日观察，以及2001年2月7日至2006年4月24日期间的对应交易日期:

负载Data_GlobalIdx2图(日期，100 *数据集。eb3m)“x”),包含(“日期”), ylabel (“日收益率(%)”)标题(3个月期Euribor日有效收益率）

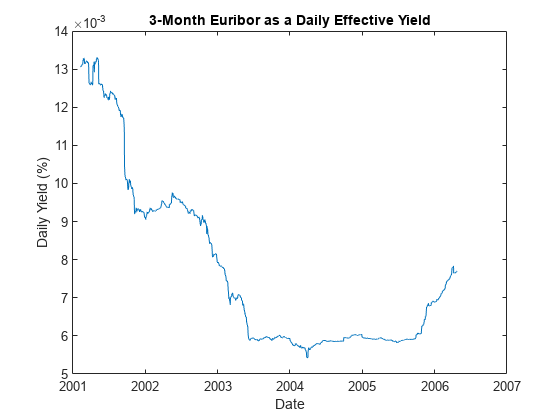
图中包含一个axes对象。标题为“3-Month Euribor as a Daily Effective Yield”的axis对象包含一个类型为line的对象。

根据数据拟合模型。现在拟合一个简单的单变量Vasicek3个月欧元银行间拆放款利率(Euribor)数据的日当量收益率模型:

$d X_{t} ＝年代（ l - X_{t} ） d t + σ d W_{t}$

给定初始条件，短期利率在某一时刻的分布T为带均值的高斯函数:

$E （ X_{T} ）＝ X_{0} e^{- 年代 T} + l （ 1 - e^{- 年代 T} ）$

和方差:

$V 一个 r （ X_{T} ）＝ σ^{2} （ 1 - e^{- 年代 T} ） / 2 年代$

为了校准这个简单的短期利率模型，用更熟悉的回归格式重写它:

$y_{t} ＝ α + β x_{t} + ε_{t}$

地点:

$y_{t} ＝ d X_{t} ， α ＝年代 l d t ， β ＝ - 年代 d t$

执行普通线性回归，其中模型波动率与残差的标准误差成正比:

$σ ＝ \sqrt{V 一个 r （ ε_{t} ） / d t}$
```
收益率=数据集。eb3m;回归系数= [ones(长度(收益率)- 1,1)收益率(1:end-1)];[系数，区间，残差]=.．.回归(diff(收益率),解释变量);Dt = 1;%时间增量= 1天速度= -coefficients(2)/dt;Level = -coefficients(1)/coefficients(2);= std(残差)/√(dt);
```

创建一个对象并设置它的初始StartState。创建一个hwv对象与StartState设置为最近观察到的短期汇率:

Obj = hwv(速度，水平，sigma，“StartState”收益率(结束)

obj = Class HWV: Hull-White/Vasicek ----------------------------------------尺寸:状态= 1,Brownian = 1 ---------------------------------------- StartTime: 0 StartState: 7.70408e-05相关性:1 Drift:漂移率函数F(t,X(t)) Diffusion:扩散率函数G(t,X(t)) Simulation:仿真方法/函数simByEuler Sigma: 4.77637e-07 Level: 6.00424e-05 Speed: 0.00228854

模拟拟合模型。例如，假设模拟的拟合模型超过64 (2⁶)交易日，使用了一种带有2次方算法的改进布朗桥，而不是通常的从头到尾蒙特卡罗模拟方法。进一步，假设初始时间和状态与历史数据最后一次可用观测的初始时间和状态一致，终点状态为未来64天后Vasicek模型的期望值。在这种情况下，您可以评估所有共享相同初始和终端状态的各种路径的行为，可能是为了支持在三个月的间隔内对路径依赖的利率选项进行定价。
创建一个插值时间向量，通过在时间上向前和向后移动来遍历时间网格。其中，第一次插补时间设置为最近的短速率观测时间，第二次插补时间设置为终端时间，后续插补次数依次采样中间状态:
```
T = 64;times = (1:T)';t = NaN(length(times) + 1,1);t(1) = obj.StartTime;t(2) = t;= T;jMax = 1;iCount = 3;为k = 1:log2(T) i = / 2;为j = 1:jMax t(iCount) = times(i);I = I +;iCount = iCount + 1;结束jMax = 2 * jMax;Delta = Delta / 2;结束
```
画出插值次数。检查由该算法生成的插值次数顺序:
```
阀杆(1:长度(t), t,“填充”)包含(“指数”), ylabel (“插补时间(天)”)标题(“二次方算法的抽样方案”）
```
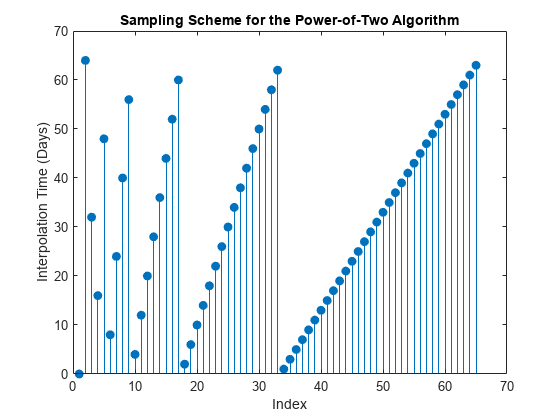
最初的几个样本在时间上被广泛分离，并决定了路径的过程结构。之后的样本间隔紧密，并逐步细化细节结构。
初始化时间序列网格。现在您已经生成了插值次数序列，初始化一个课程时间序列网格来开始插值。抽样过程开始于从历史短期利率序列中获得的最后观测时间和状态，并在未来64天后的期望值处结束Vasicek由标定参数推导出的模型:
```
平均值= obj。StartState* exp(-speed * T) + level *.．.(1 - exp(-speed * T));X = [obj]。年代t一个rt年代t一个te; average];
```
生成五个样本路径。生成五个示例路径，设置完善输入标志真正的将每一个新的插值状态插入到时间序列网格中。在试验的基础上执行插值。因为输入时间序列X是否有五个试验(其中三维时间序列的每一页代表一个独立的试验)，插值输出序列Y也有五页:
```
nTrials = 5;rng (63349“旋风”Y = obj.interpolate(t, X(:，:，ones(nTrials,1))，.．.“次”, (obj。年代t一个rtTime T],“完善”,真正的);
```
绘制结果样例路径。因为插补次数不是单调增加的，所以对插补次数进行排序，并对对应的短期汇率重新排序:
```
[t,i] = sort(t);Y =挤压(Y);Y = Y(i，:);plot(t, 100 * Y)，按住(“上”) plot(t([1端])，100 * Y([1端]，1)，”。黑色的，“MarkerSize”(20)包含“插值时间(未来天数)”) ylabel (的收益率(%)), (“关闭”)标题(“布朗桥插值的Euribor收益率”）
```
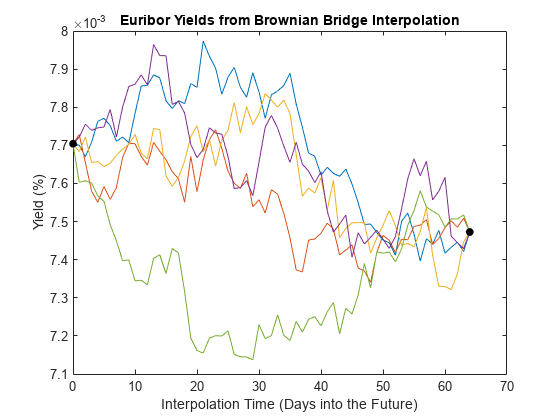
此图中的短期汇率表示共享相同初始值和终端值的备选样本路径。它们说明了一个特殊的，虽然简单的，更广泛的抽样技术的情况，称为分层抽样．有关更复杂的分层抽样示例，请参见分层抽样．
尽管这个简单的例子模拟了一个单变量Vasicek利率模型，它适用于任何维度的问题。

提示

布朗桥方法还应用了更通用的方差减少技术。有关更多信息，请参见分层抽样．

确保利率为正

所有的模拟和插值方法都允许您指定一个函数序列，或后台进程，在每个样本时间周期结束时进行评估。此期间包括由可选项确定的任何中间时间步骤NSteps输入，如在优化精度:关于解的精度和误差．这些函数被指定为时间和状态的可调用函数，并且必须返回更新后的状态向量X_t：

$X_{t} ＝ f （ t ， X_{t} ）$

必须将多个处理函数指定为函数的单元格数组。这些函数是按照它们在单元格数组中出现的顺序调用的。

处理函数不需要使用时间(t)或州(X_t)．它们也不需要更新或更改输入状态向量。事实上，模拟和插值方法不了解任何实现细节，在这方面，它们只遵循已发布的接口。

这样的处理函数提供了一个强大的建模工具，可以解决各种问题。例如，这些函数允许您指定边界条件、累积统计数据、绘制图形以及与路径相关的定价选项。

除了布朗运动(BM)模型中，模拟状态向量的单个分量通常表示的变量在现实世界中对应的变量本质上是正数，例如资产价格或利率。然而，默认情况下，这里提供的大多数模拟和插值方法都将连续采样时间之间的转换建模为缩放(可能是多元)高斯绘制。因此，在离散时间近似连续时间过程时，状态向量可能不为正。唯一的例外是simBySolution为“绿带运动”对象和simBySolution为hwv对象，可分离几何布朗运动模型的对数变换。此外，在默认情况下，仿真和插值方法都不对状态向量进行调整。因此，您有责任确保状态向量的所有分量都适当地保持为正。

幸运的是，指定非负状态确保了简单的期末处理调整。虽然这种调整是广泛适用的，但当应用到单变量时，它是揭示的圆形的平方根扩散模型:

$d X_{t} ＝０．２５（ 0．1 - X_{t} ） d t + 0.2 X_{t}^{\frac{1}{2}} d W_{t} ＝年代（ l - X_{t} ） d t + σ X_{t}^{\frac{1}{2}} d W_{t}$

也许这是单变量的主要吸引力圆形的模型的地方:

$2 年代 l \geq σ^{2}$

短期汇率保持为正。然而，短期利率的正性只适用于基础的连续时间模型。

的每日短利率圆形的模型。为了说明后一种说法，模拟日短期利率圆形的模型,使用圆形的，超过一个日历年(约250个交易日):

rng (14151617,“旋风”) obj = cir(0.25，@(t,X)0.1,0.2，“StartState”, 0.02);[X,T] = simByEuler(obj,250，“DeltaTime”, 1/250,“nTrials”5);sprintf (' % 0.4 f \ t % 0.4 f + i % 0.4 f \ n ', (T (195:205) ';.．.真正的(X (195:205 1 4)) ';图像放大(X (195:205 1 4))))

Ans = '0.7760 0.0003+i0.0000 0.7800 0.0004+i0.0000 0.7840 0.0002+i0.0000 0.7880 -0.0000+i0.0000 0.7920 0.0001+i0.0000 0.7960 0.0002+i0.0000 0.8000 0.0002+i0.0000 0.8040 0.0008+i0.0001 0.120 0.0008+i0.0001 0.8160 0.0008+i0.0001 '

如果在离散时间内模拟产生的路径，利率可能变为负值。此外,由于圆形的模型包含了平方根扩散项，短期汇率甚至可能变得复杂。

使用处理函数重复模拟。重复模拟，这次指定一个处理函数，该函数在每个周期结束时取短期汇率的绝对值。您可以按时间和状态访问处理功能(t，X_t)，但它只使用短期汇率的状态向量X_t：
```
rng (14151617,“旋风”) [Y,T] = simByEuler(obj, 2000,20)“DeltaTime”, 1/250,.．.“nTrials”，5，“过程”@ (t, X) abs (X));
```

比较调整和未调整的路径。用图形的方式比较未调整路径的大小(有负数和复数!)与在感兴趣的时间跨度内使用期末处理函数保持正的对应路径的大小:

clf情节(T, 100 * abs (X(:, 1、4)),“红色”T 100 * Y(:, 1、4),“蓝”([0.75 1 0 0.4]) xlabel(的时间(年)), ylabel (“短期利率(%)”)标题(“单变量CIR短期利率”)({传奇“负面/复杂率”“积极率”}，.．.“位置”，“最佳”）

图中包含一个axes对象。标题为Univariate CIR Short Rates的axis对象包含两个类型为line的对象。这些对象代表负/复杂比率，正比率。

提示

您可以使用此方法获得更精确的SDE解决方案。有关更多信息，请参见性能考虑．

另请参阅

钻|bm|“绿带运动”|默顿|贝茨|漂移|扩散|sdeddo|sdeld|cev|圆形的|赫斯顿|hwv|sdemrd|ts2func|模拟|simByEuler|simByQuadExp|simBySolution|simBySolution|插入

模拟利率

用插值法模拟利率

确保利率为正

另请参阅

相关的例子

更多关于