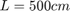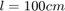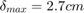用遗传算法求解混合整数工程设计问题
这个例子展示如何使用遗传算法(遗传算法)全局优化工具箱中的求解器。
本例中所说明的问题涉及阶梯悬臂梁的设计。特别是,梁必须能够承载规定的末端荷载。我们将在各种工程设计约束条件下解决一个最小化梁体积的问题。
在这个例子中,我们将解决在[1]中发布的问题的两个有界版本。
阶梯悬臂梁设计问题
在一端支撑一个阶梯悬臂梁,在自由端施加载荷,如下图所示。梁必须能够承受给定的载荷, ,在一个固定的距离
,在一个固定的距离 的支持。梁的设计者可以改变宽度(
的支持。梁的设计者可以改变宽度( )和身高(
)和身高( )。我们假设悬臂的每一部分长度相同,
)。我们假设悬臂的每一部分长度相同, .
.

光束的体积
光束的体积, 为各部分体积之和
为各部分体积之和

设计约束:1 -弯曲应力
考虑一个单一的悬臂梁,其坐标中心在其截面的中心在梁的自由端。一点处的弯曲应力 由下式给出
由下式给出

在哪里 弯矩在吗
弯矩在吗 ,
, 到末端荷载的距离和
到末端荷载的距离和 是梁的面积惯性矩。
是梁的面积惯性矩。
现在,在如图所示的阶梯悬臂梁中,梁各截面的最大弯矩为 ,在那里
,在那里 是到末端荷载的最大距离,
是到末端荷载的最大距离, ,为梁的每个截面。因此,最大应力为
,为梁的每个截面。因此,最大应力为 梁的-th截面,
梁的-th截面, ,由
,由

当最大应力发生在梁的边缘时, .面积转动惯量
.面积转动惯量 梁的-th截面由
梁的-th截面由

把这个代入方程 给了
给了

悬臂各部分的弯曲应力不应超过最大允许应力, .因此,我们最终可以陈述五个弯曲应力约束(一个用于悬臂的每一步)
.因此,我们最终可以陈述五个弯曲应力约束(一个用于悬臂的每一步)





设计约束:2 -端偏转
悬臂的末端挠度可以用Castigliano第二定理来计算,该定理指出

在哪里 是梁的挠度,
是梁的挠度, 是由于外力储存在梁中的能量,
是由于外力储存在梁中的能量, .
.
储存在悬臂梁中的能量由

在哪里 施加力的时刻是
施加力的时刻是 .
.
考虑到 对于悬臂梁,我们可以把上面的方程写成
对于悬臂梁,我们可以把上面的方程写成
![P^2/2E \int_0^l \![(x + 4 l) ^ 2 / I_1 \ & # xA;+ (x + 3 l) ^ 2 / I_2 \ & # xA;+ l (x + 2) ^ 2 / I_3 \ & # xA;+ (x + l) ^ 2 / I_4 \ & # xA;+ x^2/I_5]\, \mathrm{d} x$$](http://www.ru-cchi.com/help/examples/globaloptim/win64/steppedCantileverExample_eq17007742970191506642.png)
在哪里 面积是转动惯量吗
面积是转动惯量吗 -第一部分悬臂。对积分求值得到以下表达式
-第一部分悬臂。对积分求值得到以下表达式 .
.

应用Castigliano定理,给出了梁的末端挠度

现在,悬臂的末端挠度, ,应小于最大允许挠度,
,应小于最大允许挠度, ,得到以下约束条件。
,得到以下约束条件。

设计约束:3 -长宽比
对于悬臂的每一步,长宽比不得超过允许的最大长宽比, .也就是说,
.也就是说,
 为
为
说明优化问题
我们现在能够给出给定的约束条件,找出阶梯悬臂梁的最优参数的问题。
让 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 而且
而且
最小化:

主题:







梁的第一步只能加工到最近的厘米。也就是说, 而且
而且 必须是整数。其余的变量是连续的。变量的边界如下:-
必须是整数。其余的变量是连续的。变量的边界如下:-






该问题的设计参数
对于我们在本例中要解决的问题,梁必须支撑的端荷载为 .
.
梁的长度和最大端挠度为:
梁总长度,
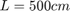
梁的单独截面,
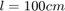
最大梁端挠度,
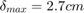
梁每一步的最大允许应力,
梁每一步的杨氏模量,
求解混合整数优化问题
我们现在解决了说明优化问题.
定义适应度和约束函数
检查MATLAB®文件cantileverVolume.m而且cantileverConstraints.m看看适应度和约束函数是如何实现的。
关于线性约束的注意事项:当线性约束指定为遗传算法,通常通过一个,b,Aeq而且说真的输入。在这种情况下,我们通过非线性约束函数来指定它们。这是因为在本例后面,一些变量将变成离散的。当问题中存在离散变量时,在非线性约束函数中指定线性约束要容易得多。另一种方法是修改线性约束矩阵以在变换后的变量空间中工作,这不是简单的,也许是不可能的。同样,在混合整数中遗传算法在求解器中,线性约束与非线性约束的处理没有任何区别,无论它们是如何指定的。
设置范围
创建包含下界(磅)和上限约束(乌兰巴托).
Lb = [1 30 2.4 45 2.4 45 1 30 1 30];Ub = [5 65 3.1 60 3.1 60 5 65 5 65];
设置选项
为了得到更精确的解,我们增加PopulationSize,MaxGenerations选项从默认值中删除,并减少EliteCount而且FunctionTolerance选项。这些设置的原因遗传算法使用更大的种群(增加PopulationSize),增加设计空间的搜索(减少EliteCount),并继续进行,直到其最佳成员的变化非常小(小FunctionTolerance)。我们还指定了一个plot函数来监视惩罚函数的值遗传算法的进展。
注意,这里有一组受限的遗传算法在解决混合整数问题时可用的选项-有关更多细节,请参阅全局优化工具箱用户指南。
选择= optimoptions (@ga,...“PopulationSize”, 150,...“MaxGenerations”, 200,...“EliteCount”10...“FunctionTolerance”1 e-8...“PlotFcn”, @gaplotbestf);
调用遗传算法解决问题
我们现在可以叫遗传算法解决问题。在问题陈述中 而且
而且 是整数变量。我们通过传递索引向量来指定它
是整数变量。我们通过传递索引向量来指定它(1 2)来遗传算法在非线性约束输入之后,在选项输入之前。为了再现性,我们还在这里设置了随机数生成器。
rng (0,“旋风”);[xb, fb, exitflag] = ga (@cantileverVolume 10 , [], [], [], [],...lb, ub, @cantileverConstraints, [1 2], opts);
优化终止:超过最大代数。

分析结果
如果一个问题有整数约束,遗传算法哈贝马斯在内部。特别地,问题中的适应度函数被一个处理约束的惩罚函数所取代。对于可行的总体成员,惩罚函数与适应度函数相同。
返回的解遗传算法如下显示。注意,最靠近支撑的部分被限制为宽度( )和身高(
)和身高( ),它是一个整数值,并且该约束已被GA所遵守。
),它是一个整数值,并且该约束已被GA所遵守。
显示(xb);
xbest =第1 ~ 7列3.0000 60.0000 2.8504 57.0057 2.6114 50.6243 2.2132第8 ~ 10列44.2349 1.7543 35.0595
我们也可以问遗传算法返回光束的最佳体积。
流(ga = %g\n'返回的cost函数、fb);
ga返回的代价函数= 63408.9
添加离散非整数变量约束
工程师们现在被告知,悬臂的第二步和第三步的宽度和高度只能从标准集合中选择。在本节中,我们将展示如何将此约束添加到优化问题中。注意,添加了这个约束后,这个问题与在[1]中解决的问题相同。
首先,我们说明将添加到上述优化的额外约束
梁的第二步和第三步的宽度必须从以下集合中选择:- [2.4,2.6,2.8,3.1]cm
梁的第二步和第三步的高度必须从以下集合中选择:- [45,50,55,60]cm
要解决这个问题,我们需要能够指定变量 ,
, ,
, 而且
而且 离散变量。要指定一个组件
离散变量。要指定一个组件 从集合中取离散的值
从集合中取离散的值 、优化与
、优化与 取从1到的值的整数变量
取从1到的值的整数变量 ,并使用
,并使用 作为离散值。指定范围(1到
作为离散值。指定范围(1到 ),设1为下界
),设1为下界 作为上界。
作为上界。
首先,我们变换离散变量的边界。每个集合有4个成员,我们将离散变量映射到范围[1,4]的整数。为了将这些变量映射为整数,我们将每个变量的下界设为1上界设为4。
Lb = [1 30 1 1 1 1 1 30 1 30];Ub = [5 65 4 4 4 4 5 65 5 65];
的转换(整数)版本 ,
, ,
, 而且
而且 现在将传递给适应度和约束函数,当
现在将传递给适应度和约束函数,当遗传算法解算器。为了正确计算这些函数, ,
, ,
, 而且
而且 需要在这些函数中转换为给定离散集的一个成员。要了解这是如何实现的,请检查MATLAB文件
需要在这些函数中转换为给定离散集的一个成员。要了解这是如何实现的,请检查MATLAB文件cantileverVolumeWithDisc.m,cantileverConstraintsWithDisc.m而且cantileverMapVariables.m.
现在我们可以调用遗传算法解决离散变量问题。在这种情况下 都是整数。这意味着我们要传递索引向量
都是整数。这意味着我们要传递索引向量1:6来遗传算法来定义整数变量。
rng (0,“旋风”);[xbestDisc, fbestDisc, exitflagDisc] = ga(@cantileverVolumeWithDisc,...10, [], [], [], [], lb, ub, @cantileverConstraintsWithDisc, 1:6, opts);
优化终止:超过最大代数。

分析结果
xbestDisc(三6)是回来遗传算法整数形式(即转换后的状态)。我们需要反向变换来检索他们工程单位中的值。
xbestDisc = cantileverMapVariables (xbestDisc);显示(xbestDisc);
xbestDisc =列1 ~ 7 3.0000 60.0000 3.1000 55.0000 2.6000 50.0000 2.2430列8 ~ 10 44.8603 1.8279 36.5593
和前面一样,解返回遗传算法遵守约束条件 而且
而且 都是整数。我们也可以看到
都是整数。我们也可以看到 ,
, 从[2.4,2.6,2.8,3.1]cm和
从[2.4,2.6,2.8,3.1]cm和 ,
, 从[45,50,55,60]cm中选择。
从[45,50,55,60]cm中选择。
回想一下,我们在变量上添加了额外的约束x (3),x (4),x (5)而且x (6).正如预期的那样,当对这些变量有额外的离散约束时,最优解具有更高的最小体积。请进一步注意,[1]中报告的解决方案的最小体积为 我们找到了一个近似于[1]中报告的解。
我们找到了一个近似于[1]中报告的解。
流(ga = %g\n'返回的cost函数, fbestDisc);
ga返回的代价函数= 64795
总结
这个例子说明了如何使用遗传算法求解器,遗传算法,求解具有整数约束的有约束非线性优化问题。该示例还展示了如何处理在问题表述中具有离散变量的问题。
参考文献
Thanedar, P. B.和G. N. Vanderplaats。结构设计中的离散变量优化研究综述结构工程学报,1995,(3),pp. 301-306。