利用优化变量拟合ODE参数

这个例子展示了如何使用优化变量(基于问题的方法)在最小二乘意义下找到优化常微分方程(ODE)的参数。

问题

这个问题是一个多步反应模型，涉及几种物质，其中一些物质相互反应产生不同的物质。

对于这个问题，真实的反应速率是未知的。所以，你需要观察反应并推断反应速率。假设你可以测量一组时间的物质 $t$ ．从这些观察中，拟合最佳的反应速率集的测量。

模型

这个模型有六种物质， $C_{1}$ 通过 $C_{6}$ ，其反应如下:

一个 $C_{1}$ 和一个 $C_{2}$ 反应形成一个 $C_{3.}$ 在速度 $r_{1}$
一个 $C_{3.}$ 和一个 $C_{4}$ 反应形成一个 $C_{5}$ 在速度 $r_{2}$
一个 $C_{3.}$ 和一个 $C_{4}$ 反应形成一个 $C_{6}$ 在速度 $r_{3.}$

反应速率与所需物质数量的乘积成正比。所以,如果 $y_{我}$ 表示物质的数量 $C_{我}$ ，则反应速率产生 $C_{3.}$ 是 $r_{1} y_{1} y_{2}$ ．类似的，反应速率 $C_{5}$ 是 $r_{2} y_{3.} y_{4}$ 和反应速率 $C_{6}$ 是 $r_{3.} y_{3.} y_{4}$ ．

换句话说，控制系统演化的微分方程是

$\frac{dy}{dt} ＝［ \begin{matrix} - r_{1} y_{1} y_{2} \\ - r_{1} y_{1} y_{2} \\ - r_{2} y_{3.} y_{4} + r_{1} y_{1} y_{2} - r_{3.} y_{3.} y_{4} \\ - r_{2} y_{3.} y_{4} - r_{3.} y_{3.} y_{4} \\ r_{2} y_{3.} y_{4} \\ r_{3.} y_{3.} y_{4} \end{matrix} ］．$

微分方程在0时刻的某一点开始 $y （ 0 ）＝［ 1 ， 1 ， 0 ， 1 ， 0 ， 0 ］$ ．这些初始值确保所有物质完全反应，导致 $C_{1}$ 通过 $C_{4}$ 渐近:随着时间的增加而趋于零

MATLAB中的表达式模型

的diffun函数实现微分方程的一种形式，可以通过数值．

类型diffun

函数dydt = diffun(~，y,r) dydt = 0 (6,1);s12 = y y (1) * (2);s34 = y (3) * y (4);dydt (1) = - r (1) * s12;dydt (2) = - r (1) * s12;Dydt (3) = -r(2)*s34 + r(1)*s12 -r(3)*s34;Dydt (4) = -r(2)*s34 -r(3)*s34;dydt (5) = r (2) * s34;dydt (6) = r (3) * s34;结束

真实的反应速率是 $r_{1} ＝ 2 ． 5$ ， $r_{2} ＝ 1 ． 2$ , $r_{3.} ＝ 0 ． 45$ ．计算系统从0到5的演化，调用数值．

Rtrue = [2.5 1.2 0.45];Y0 = [1 1 0 1 0 0];tspan = linspace (0 5);soltrue =数值(@ (t, y) diffun (t y rtrue) tspan, y0);yvalstrue =德瓦尔(soltrue tspan);为I = 1:6 subplot(3,2, I) plot(tspan,yvalstrue(I，:)) title([“y(”num2str(我),“)”])结束

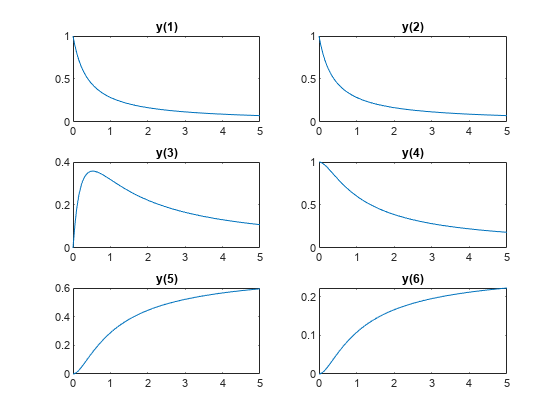
图中包含6个轴对象。标题为y(1)的axis对象1包含一个类型为line的对象。标题为y(2)的Axes对象2包含一个类型为line的对象。标题为y(3)的Axes对象3包含一个类型为line的对象。标题为y(4)的Axes对象4包含一个类型为line的对象。标题为y(5)的axis对象5包含一个类型为line的对象。标题为y(6)的axis对象6包含一个类型为line的对象。

优化问题

为了在基于问题的方法中为解决问题做好准备，创建一个三元素优化变量r它的下界是0．1的上限10．

r = optimvar (“r”3,“下界”, 0.1,“UpperBound”10);

该问题的目标函数是ODE解与参数的差的平方和r还有带真参数的解yvals．为了表达这个目标函数，首先编写一个MATLAB函数，使用参数计算ODE的解r．这个函数是RtoODE函数。

类型RtoODE

函数solpts = RtoODE(r,tspan,y0) sol = ode45(@(t,y)diffun(t,y,r)，tspan,y0);solpts =德瓦尔(溶胶,tspan);结束

使用RtoODE在目标函数中，将函数转换为优化表达式fcn2optimexpr．看到将非线性函数转化为优化表达式．

myfcn = fcn2optimexpr (@RtoODE r tspan, y0);

将目标函数表示为ODE解与带真参数解的差的平方和。

Obj = sum(sum((myfcn - yvalstrue).^2));

用目标函数创建一个优化问题obj．

概率= optimproblem (“客观”、obj);

解决问题

求最佳拟合参数r，给出一个初步的猜测r0为求解器和调用解决．

r0。r＝［111］; [rsol,sumsq] = solve(prob,r0)

使用lsqnonlin解决问题。局部最小值。由于梯度的大小小于最优公差值，因此优化已完成。

rsol =结构体字段:r (3 x1双):

sumsq = 3.8659 e15汽油

差的平方和基本上为零，这意味着求解器找到了使ODE解与真参数匹配的参数。因此，正如预期的那样，解包含真实的参数。

disp (rsol.r)

2.5000 1.2000 0.4500

disp (rtrue)

2.5000 1.2000 0.4500

有限的观察

假设你不能观察到的所有组成部分y，但只有最终的输出y (5)而且y (6)．根据这些有限的信息，你能得到所有反应速率的值吗?

要找出答案，修改函数RtoODE只返回第五个和第六个ODE输出。引入了改进的ODE求解器RtoODE2．

类型RtoODE2

函数solpts = RtoODE2(r,tspan,y0);solpts = solpts((5、6):);只有y(5)和y(6)结束。

的RtoODE2函数简单地调用RtoODE然后取输出的最后两行。

创建一个新的优化表达式RtoODE2优化变量r，时间跨度数据tspan，和初始点y0．

myfcn2 = fcn2optimexpr (@RtoODE2 r tspan, y0);

修改比较数据，只包括输出5和6。

yvals2 = yvalstrue((5、6):);

从优化表达式中创建新的目标和新的优化问题myfcn2对比数据yvals2．

Obj2 = sum(sum((myfcn2 - yvals2).^2));prob2 = optimproblem (“客观”, methoda);

根据这些有限的观察结果来解决问题。

[rsol2, sumsq2] =解决(prob2 r0)

使用lsqnonlin解决问题。局部最小值。Lsqnonlin停止了，因为相对于其初始值的平方和的最终变化小于函数公差的值。

rsol2 =结构体字段:r (3 x1双):

sumsq2 = 2.1616 e-05

同样，返回的平方和本质上是零。这是否意味着求解器找到了正确的反应速率?

disp (rsol2.r)

1.7811 1.5730 0.5899

disp (rtrue)

2.5000 1.2000 0.4500

没有;在这种情况下，新汇率与真实汇率相差很大。然而，新的ODE解与真实值的对比图表明y (5)而且y (6)匹配真实值。

图绘制(tspan yvals2 (1:)“b -”)举行在ss2 = RtoODE2 (rsol2.r tspan, y0);:情节(ss2 tspan, (1),“r——”)情节(tspan yvals2 (2:)“c -”ss2)情节(tspan (2:)“m——”)传说(“真正y (5) '，“新y(5)”，“真正y (6) '，“新y(6)”，“位置”，“西北”)举行从

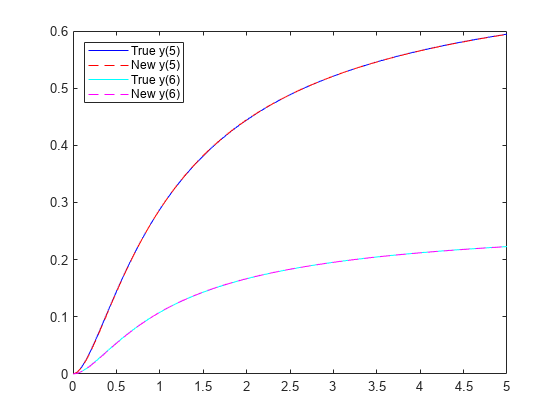
图中包含一个axes对象。axis对象包含4个line类型的对象。这些对象表示True y(5)， New y(5)， True y(6)， New y(6)。

要确定这个问题的正确反应速率，你必须有更多的观察数据y (5)而且y (6)．

用新参数画出解的所有分量，用真参数画出解。

图yvals2 = RtoODE(rsol2.r,tspan,y0);为I = 1:6 subplot(3,2, I) plot(tspan,yvalstrue(I，:)，“b -”、tspan yvals2(我,:),“r——”)传说(“真正的”，“新”，“位置”，“最佳”)标题(“y(”num2str(我),“)”])结束

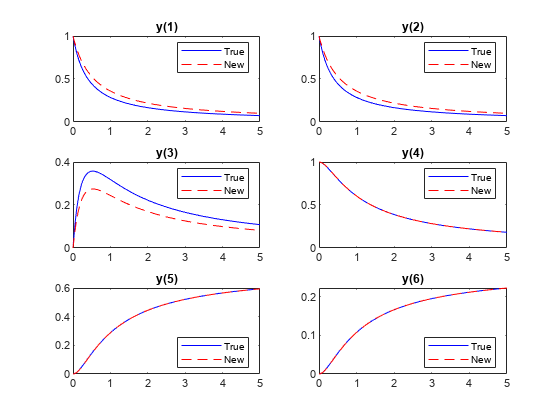
图中包含6个轴对象。标题为y(1)的axis对象1包含两个类型为line的对象。这些对象表示True、New。标题为y(2)的axis对象2包含两个类型为line的对象。这些对象表示True、New。标题为y(3)的axis对象3包含两个类型为line的对象。这些对象表示True、New。标题为y(4)的axis对象4包含两个类型为line的对象。这些对象表示True、New。标题为y(5)的axis对象5包含两个类型为line的对象。 These objects represent True, New. Axes object 6 with title y(6) contains 2 objects of type line. These objects represent True, New.

有了新的参数，物质 $C_{1}$ 而且 $C_{2}$ 沥干得更慢，物质也更丰富 $C_{3.}$ 不会积累那么多。但物质 $C_{4}$ ， $C_{5}$ , $C_{6}$ 新参数和真参数都有完全相同的演化过程。

另请参阅

解决|数值|fcn2optimexpr